Calculator MAY be used to help answer this question.
Be certain to limit yourself to the four permissible calculator functions.
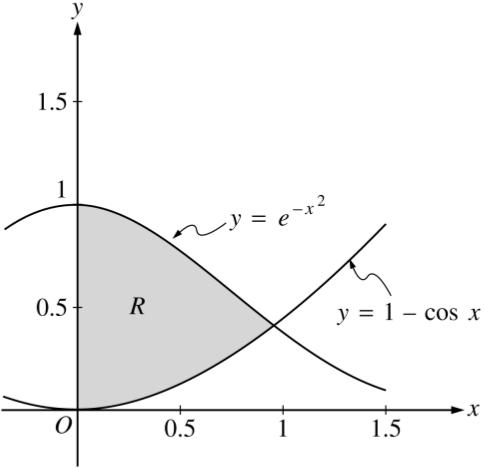
Let R be the shaded region in the first quadrant enclosed by the graphs of  ,
,  , and the y-axis, as shown in the figure at right.
, and the y-axis, as shown in the figure at right.
(a) Find the area of region R.
(b) Find the volume of the solid generated when the region R is revolved about the line y = -1.
(c) The region R is the base of a solid. For this solid, each cross section perpendicular to the x-axis is an equilateral triangle. Find the volume of this solid.
Quick Find Code For This Problem.
Legend: [QUES5LGND]
Solution For Part a.): [QUES5PA]
Solution For Part b.): [QUES5PB]
Solution For Part c.): [QUES5PC]
How To Use Quick Find.
-To Use Quick Find, copy (Ctrl+C/Command+C) the code (All the stuff INSIDE the square brackets in the code region above) for which ever section you'd like to go to, then, hit in this order;
Ctrl+F
Ctrl+V
Enter/Return
or if your on a Mac You'd hit
Command+F
Command+V
Enter/Return.
Then, your webbrowser should bring you directly to the beginning of the solution indicated by the code, making navigation through longish solutions much easier. Enjoy :]
[QUES5LGND]
LEGEND
GREEN = CALCULATOR INSTRUCTIONS
BLUE = IMPORTANT NOTES/LINKS
RED = STUFF THAT NEEDS TO BE FOUND TO HELP SOLVE QUESTION
PURPLE = STEPS TAKEN
The four permissible (TI-83) calculator functions that we're allowed to use to solve these wiki questions:
- Graphing the function: [Y=] [GRAPH]
- Determining the roots or y-intercepts: [2nd] [CALC] [2:zero]
- Numerically differentiating a function: [2nd] [6:dy/dx] or [MATH] [8:nDeriv]
- Numerically integrating a function: [2nd] [7:∫f(x)dx] or [MATH] [9:fnInt]
Solution
[QUES5PA]
(a) GIVEN FROM QUESTION ARE:  AND
AND 
Intersects must be found so that they can be used as limits for the integral, or from which points the area of the region shall be calculated. In order to do that;



Normally I would algebraically solve for the intersects by making the two equations equal to each other and solve for x. But because e to the negative x squared is such a monster to deal with, it leads to a dead end.
Since this is a transcendental function, a function that contains an exponential function and a trigonometric function, we can’t apply the algebra we know to solve for the roots, so we have to use our calculator.
Plug the two functions SEPARATELY into Y variables...in Y1 and Y2. Then press 2nd Calc 5 for the intersect function. Looking at the graph, we see R is bounded at x = 0 and at x = ???, where ??? is the x-coordinate of where the two functions intersect.
Since the algebraic way to find intersects by making them equal to each other isn't working, I also tried massaging it a little by moving the terms to one side and finding the roots.

Using the calculator to determine the roots of e^(-x^2) + cos(x) - 1 = 0, I obtain x = 0.9419441. Although this isn't the only intercept, x = 0.9419441, we're only interested in the intercept that's close x = 1, because that's where the x-coordinate of the point of intersection is. We can see this on the graph as well.

e^(-x^2) + cos(x) - 1 = 0 at x = 0.9419441
Therefore...

Using fnInt function in our calculator, we obtain A = 0.59096245.
[QUES5PB]
(b) To find volume there is usually a general formula. I don't like using that term now. I prefer the word, PATTERN.
When an area is being rotated around the x-axis, the general formula is:

Because the area is revolving around the axis, it forms a washer shape. To get the volume, we integrate the area given. R is the bigger radius, and is the upper function and could also be looked at as f(x) and the lower function, g(x) is the smaller radius. This lower function forms the "hole" in the washer.
For visual representation, refer to this diagram, which is looking at the function from a different side; a different perspective.It is important to visually see the actual shape, because it REALLY helps when revolving a 2D object and pretending as if it was three dimensional.

The upper function in this problem is  . The lower function or radius is
. The lower function or radius is  . Therefore
. Therefore

The reason why each radius has a "+1" added, is because the area is not being revolved exactly on the axis, but rather, one unit below the axis, therefore from each radius, -1 is subtracted. Two negatives of course makes a postive. This can be simplified to:
Usually I would antidifferentiate the monster of an equation and plug in the limits to find the integral and find the difference between the result of plugging the upper and lower limits in, but  can't be antidifferentiated using the algebra we know, so I'm just going to plug this equation into my calculator and use the "fnInt" function to integrate from -0.91419441 to 0.91419441.
can't be antidifferentiated using the algebra we know, so I'm just going to plug this equation into my calculator and use the "fnInt" function to integrate from -0.91419441 to 0.91419441.
**To use the fnInt function on my calculator:
- Put the equation in Y1
- Quit to the home screen ["2ND" + "MODE"]
- Between the brackets, separated with commas, put equation, variable, lower limit and upper limit. [VARS Y1, X, 0, 0.91419441] OR plug and chug everything into fnInt:

Then the sum will be found for you. This leaves us with:
V= 5.454328983 units cubed
For more on the washer method and volumes of revolving objects, perhaps take a peek at this.
[QUES5PC]
(c) Firstly, the question states that the shaded region is the base of the solid. One face of the solid is said to be the shape of an equilateral triangle, as are the other faces of each cross section.
It's important to remember that the area of a triangle is equal to 1/2 (base)(height).

This is visual representation of what a cross section would look like. The height isn't given so in order to find it, some trigonometry is involved.

In order to find the actual value of the height, you can either use the pythagorean theorem or even any of the trigonometric ratios that can be used to find the side of a right triangle.
A side note is that we know all equilateral triangles have sides that are equal in length as well as the size angles. The angles in equilateral triangles are all equal to  .
.
The height is positioned opposite the angle. Therefore, it is true to say that:

Since the sine of an angle is opposite/hypotenuse. h is opposite the angle and the expression is the hypotenuse. In order to find the value for h, it must be isolated.
Now that the height is found and the other variables needed to find the volume of the cross section are given, plug in the values known as the base, height and width for this question.

V = 0.9387 units cubed.
BOOMDEYADA~!
Comments (3)
Jamie said
at 8:37 pm on Apr 13, 2009
i don't care.. i'm claiming this question through comments section.. because.. well. it's not letting me edit anything. as for notation, i'll fix that later. when my account isn't being.. GRR.
a)must find where intersection occurs, so that it can also be labelled as a limit.
- in order to find that, you can make
e^(-x^2) = 1 - cos x
e^(-x^2) cos x = 1[using the identity]
-x^2 cos x = ln 1
-x^2 cos x = 0
- (x^2 cos x) = 0
oy.... dead end.. i know i didn't get this right.. but i have a week. I'm claiming this question... haha.
[find the intersections. I sometimes have trouble with this...]
then... when the intersections are found.. it's as simple as AREA = integral of upper - lower function from LIMITS that are provided by the intersections.
therefore A = integral from e^(-x^2) - 1 - cos x
b) V = pi integral [from limits A - B] [(1-e^(-x^2))^2 - (1-1-cos x)^2] dx
... to be continued....
Jamie said
at 8:58 pm on Apr 13, 2009
ooh i know where i messed up.. and i should continue.. but i can't.....**anxiously waits for edit button to work... **
Kristina said
at 5:04 pm on Apr 14, 2009
I know how you feel now, the edit button isn't working for me either. >__> ....At least I "claimed" my question though lol
You don't have permission to comment on this page.