A Calculator MAY NOT be used to help answer this question.
The figure shows ƒ', the derivative of a function ƒ.
The domain of the function ƒ is the interval [0, 20].

(a) For what values of x, 0 < x < 20, does ƒ have a relative maximum? Justify your answer.
(b) For what values of x is the graph of ƒ concave down? Justify your answer.
(c) If ƒ(0) = 10, sketch a graph of the function ƒ on axes similar to the ones provided below. List the coordinates of all critical points and inflection points.

Quick Find Code For This Problem.
Legend: [QUES7LGND]
Solution For Part a.): [QUES7PA]
Solution For Part b.): [QUES7PB]
Solution For Part c.): [QUES7PC]
Solutions For All Parts: [QUES7ANS]
How To Use Quick Find.
-To Use Quick Find, copy (Ctrl+C/Command+C) the code (All the stuff INSIDE the square brackets in the code region above) for which ever section you'd like to go to, then, hit in this order;
Ctrl+F
Ctrl+V
Enter/Return
or if your on a Mac You'd hit
Command+F
Command+V
Enter/Return.
Then, your webbrowser should bring you directly to the beginning of the solution indicated by the code, making navigation through longish solutions much easier. Enjoy :]
Solution
[QUES7LGND]
Text in purple will be used primarily to connotate steps/information that are necessary to solving the problem.
Text in light blue will be used to connotate things that one should note, or that may be of some kind of importance.
Text in black is more or less just background banter.
Text in black that is emboldened will be used solely for the questions themselves.
Text in green is used to connotate the answer to a problem.
The figure shows ƒ', the derivative of a function ƒ.
The domain of the function ƒ is the interval [0, 20].
[QUES7PA]
Part A.) For what values of x, 0 < x < 20, does ƒ have a relative maximum? Justify your answer.
The solution of part a is for the most part a straight forward application of the first derivative test.
http://en.wikipedia.org/wiki/First_derivative_test
The first step to solving this problem is to find the critical numbers of the graph.
By definition the critical numbers of a derivative are where the derivative is either zero, or undefined.

On the sample graph provided these points are located at
0, 5, 10, 12.5 and 15
(because at those points, the derivative of f, illustrated in the graph is either zero, or undefined.)
However, the domain supplied by the problem eliminates 0 as a possible relative maximum or minimum and thus we are left with 5, 10, 12.5 and 15 as our critical numbers. Now to figure out if these points [(5,0), (10,0), (12.5,0) and (15,0) ] are relative maximums or not, we need to look at their context,
that is to say, whats around these points.

On this graph, everything in the blue region is positive, and everything in the red region is negative.
We combine this knowledge with our location of the critical numbers to begin to figure out if those points are relative minimums or maximums.
Looking to the left of (10,0), the graph of f’(x) is positive, to the right of (10,0) it is negative.
This means, that on the parent graph, the slope at the point to the left of the graph is positive, and on the right negative. This suggests that f(10) is a maximum. Now by the same process we check the second critical number at (15,0) and find that to the left of this point, the first derivative is negative and to the right of this point, the first derivative is positive.
The critical numbers at (5,0) and (12.5) are different. Looking to the left of (5,0) we see that f'(x) is positive. Looking to the right also yields the same result. Thus (5,0) is neither a relative minimum or maximum. What it is exactly, will be dealt with later. The same process reveals that at (12.5, 0) f'(x) is also negative both to the left and right and therefore it neither, is a relative min or max.
Thus we can say, by the first derivative test, f(10) is a relative maximum, and also by the first derivative test, f(15) is a relative minimum
[QUES7PB]
Part B.) For what values of x is the graph of ƒ concave down? Justify your answer.
This question is another straight forward application of one of the derivative tests, in this case, the second derivative test
http://en.wikipedia.org/wiki/Second_derivative_test
Sketching out the graph of f’’(x) we find that the result is a peace wise graph, with two portions in the positive section, and one in the negative section.

Here is an excerpt from wikipedia which will explain how we will use the second derivative test to determine concavity;
"The second derivative test may also be used to determine the concavity of a function as well as a function's points of inflection.
First, all points at which  are found. In each of the intervals created,
are found. In each of the intervals created,  is then evaluated at a single point. For the intervals where the evaluated value of
is then evaluated at a single point. For the intervals where the evaluated value of 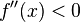 the function
the function  is concave down, and for all intervals between critical points where the evaluated value of
is concave down, and for all intervals between critical points where the evaluated value of  the function
the function  is concave up. The points that separate intervals of opposing concavity are points of inflection."
is concave up. The points that separate intervals of opposing concavity are points of inflection."
As mentioned in the wikipedia excerpt, the first thing to do is find all points at which f'(x) = 0. We've already done this in Part. A.) and know these points to be
f'(10)=0 and f'(15)=0 (10 and 15)

On the colourful graph above we see a bunch of colored "zones". These are the intervals we will use to determine concavity. The two red lines represent the critical points, (10,0) and (15,0). We also see that our oddball critical points, 5 and 12.5 are divisions for a zone as well. So now, lets get onto reading this graph.
According to the second derivative test, if f''(x) > 0 then f(x) is concave up. If f''(x) is < 0 then f(x) is concave down. If f''(x) = 0 then you cannot tell what is going on, and if f''(c) is undefined then there is an inflection point at c. Knowing this, we can begin to decode the graph.
At the critical point 10, f''(x) is negative(<0). Thus at x = 10, f(x) is concave down.
At the critical point 15, f''(x) is positive (>0). Thus at x = 15, f(x) is concave up.
This means that somewhere in the interval between x = 10 and x = 15 f(x) changes concavity. Therefore we know that somewhere in there, an inflection point exists. From out knowledge that the graph of f'(x) is undefined at x = 12.5, we can say that there is an inflection point at x = 12.5.
Using a similar method of examination we find that at the critical point x = 5, there is also another inflection point.
Concavity of a function can also be found using the first derivative.
If a function is concave down, f'(x) is also decreasing.
f'(x) is shown to be decreasing in the graph from 5 ≤ x ≤ 12.5.
Therefore, f(x) is concave down from 5 ≤ x ≤ 12.5
Putting this all together we find our answer.
f(x) is concave up for 0 ≤ x ≤ 5
f(x) is concave down for 5 ≤ x ≤ 12.5
f(x) is concave up for 12.5 ≤ x ≤ 20
[QUES7PC]
Part C.) If ƒ(0) = 10, sketch a graph of the function ƒ on axes similar to the ones provided below. List the coordinates of all critical points and inflection points.
Sketching the graph of f is for the most part, a process of reverse engineering the graph of f'(x) using the concavity information and critical numbers you collected from parts a, and b.

Thanks to our examination of the second derivative, we know that there are two inflection points, one at x = 5 and another at x = 12.5. This provides us the beginnings of a framework on which we can build our graph, since we know that at those points the graph of f(x) changes concavity.

Continuing the construction of our framework we place our critical points, based on the graph of f'(x) which show where f(x) has either a local minimum or maximum. We know these to be located at x = 0, x = 10 and x = 15.

Finally, we have concavity which we found on the second derivative.
f(x) is concave up for 0 ≤ x ≤ 5
f(x) is concave down for 5 ≤ x ≤ 12.5
f(x) is concave up for 12.5 ≤ x ≤ 20

Because we know which intervals have what concavity, we can begin to connect the dots, going from critical point, to inflection point, to critical point, etc. following the concavity we know the graph should have, until we have the whole graph of f(x).

Finally to answer the question, we must list the locations of all points of inflection, and critical points.
Inflection Points located at;
x = 5
x = 12.5
Critical Points
x = 0
x = 10
x = 15
[QUES7ANS]
In Summary, the answers to the question 7 is as follows.
Part A.)
By the first derivative test, f(10) is a relative maximum, and also by the first derivative test, f(15) is a relative minimum
Part B.)
f(x) is concave up for 0 ≤ x ≤ 5
f(x) is concave down for 5 ≤ x ≤ 12.5
f(x) is concave up for 12.5 ≤ x ≤ 20
Part C.)
Inflection Points located at;
x = 5
x = 12.5
Critical Points
x = 0
x = 10
x = 15
And that is how you solve question 7.
Information/Idea Sources
en.wikipedia.org
http://www.math.hmc.edu/calculus/tutorials/secondderiv/
Formatting Ideas Credit to Benchman :] (Thanks bud ;p)